中学2年生2学期期末
今回は特に参考資料は作らず!!
提出物を早めに終わらせる予定が英語だけ残っていた
ふ~~~~~~
3日目は数学・英語・理科
難関だ!!
時間がないし集中力ももたない!!
でそうなところを抜粋で乗り切る!!
試験は今日で終わりだが3学期の期末のことを考えると今からしておかないと・・・。
範囲が広く絶対に間に合わない!!
さて、どうやって勉強をさせるかですね!!
今回は特に参考資料は作らず!!
提出物を早めに終わらせる予定が英語だけ残っていた
ふ~~~~~~
3日目は数学・英語・理科
難関だ!!
時間がないし集中力ももたない!!
でそうなところを抜粋で乗り切る!!
試験は今日で終わりだが3学期の期末のことを考えると今からしておかないと・・・。
範囲が広く絶対に間に合わない!!
さて、どうやって勉強をさせるかですね!!
無知の知について会話しました
無知の知にはいろいろ解釈があると思いますが
今回話したのは
自分が知らないことを知るという内容です
意味からは少し外れているかもしれませんが
「わからない」と聞いて答えを聞いて書く事を繰り返していても勉強にはならない
なぜわからないかを考えると言うこと
例えば
数学なら
問題の意味がわからない
公式がわからない
計算方法がわからない
答えの書き方がわからない
など
わからないところ見つける
これが肝心だと思います
子供曰く「いつになったらそういう風なれるの?大人になったらできる?」
「子供でも大人でもできる!!大人になってもできない人はいる」と答えました
「どうやったら身につくのかと」聞かれたので「日頃から何をするにもなぜそれをしたか理由を考えながら行動すれば身につくと」答えました
これから少しずつ実践するそうです!!
ちなみに恥ずかしながら今までまちがえて覚えていたものがあります
例えば
こむら返りをコブラがえり
ぎっくり腰をびっくりごし
したけのいしづきをしたけのいしづち
クリームパンダをクリームパンナ(アンパンマンのキャラクター)
一応やっておきますを一様やっておきます
私市(きさいち)私部(きさべ)をしいちとしべなど地名はことごとく違っていました
こんなことも知らないのに子供にそんなことも知らないのかと馬鹿にしていたなんて
恥ずかしい~~~~!!
試験が終わり
これから1か月は学校の勉強も少し手を抜く時期です
ただ、時間も空いてくるので今が勉強のチャンスです
まず、1年間の復習をして2年生の予習です
計画としては
英語
単語・熟語を覚える
勉強方法は単語帳に書いて毎日繰り返す
たまにテスト
できればたくさん覚えておく方がいいですね
数学
図形と関数と割合を徹底的に理解する
勉強方法は薄い問題集を完全に理解するまで繰り返しする
理科
今までの総復習
勉強方法はもう一度まとめてみる
社会
地理は総復習
勉強方法はもう一度まとめてみる
歴史は年号と重要語句を覚える
重要語句は内容まで把握すること
勉強方法は年号と重要語句を単語帳に書いて繰り返し覚える
できれば飛鳥時代~昭和までやってしまう事がいい
国語
漢字を覚える
勉強方法は漢字検定の問題集をやってみる
※来年度は少し勉強量が増えるのでこの1か月頑張れば2年生になっても勉強が嫌にならないだろうと思います
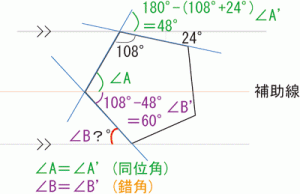
?°の所を求める問題です
まず、5角形の内角の和は180°×(5-2)=540°
ひとつの角は540°÷5=108°
まず?°を求めるには補助線を引いて錯角や同位角で求めれるようにする
?°を求めるには錯角である∠B’を求める必要がある
∠B’を求めるには∠Aを求める必要がある
∠Aを求めるには∠A’を求める必要がある
ただ、補助線を引かなくてもできる方法
まず、5角形の内角の和は180°×(5-2)=540°
ひとつの角は540°÷5=108°
上の線と正五角形の線が重なっていると考えると
下の角を挟む角は同じ角度になるので
180°-108°=72°
72°÷2=36°
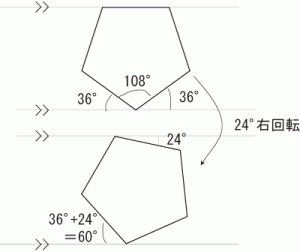
正五角形が24度回転したと考えれば
36°+24°=60°となる
備考
n角形の内角の和は180°×(n-2)
nの中には三角形がn-2個出来るからです
外角の和は必ず360°になります
昨年は合計で400人今年は男子が6%減少し、女子は18%増加した
全体で12人増えた
|
男子
|
女子
|
合計
|
|
|
昨年
|
X
|
400-X
|
400
|
|
今年
|
(1-0.06)X
|
(1+0.18)(400-X)
|
412
|
|
差
|
-0.06X
|
0.18(400-X)
|
12
|
昨年の男子をXとしたら昨年の女子は400-X
男子は6%減ったので-0.06X
女子は18%増えたので0.18(400-X)
去年より12人増えたので
-0.06X+0.18(400-X)=12
X=250
昨年の男子は250人
昨年の女子は150人
今年は男子は250×(1-0.06)=235(人)
今年は女子は150×(1+0.18)=177(人)
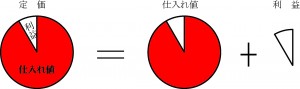
120円の定価で20円の利益を足していたら仕入れ値は100円
120-20=100(円)
仕入れ値100円に20%(2割)の利益を足した定価は120円
100×0.2=20 100+20=120(円) 又は100×(1+0.2)=120(円)
定価120円で仕入れ値に20%(2割)の利益を足していたら仕入れ値は100円
120÷(1+0.2)=100(円)
方程式 距離と速さと時間の問題はパターンAとパターンBしかない
まず、問題を読んでパターンAかパターンBになるかを考える
パターンA
同じ出発地点で同じ方向に進む
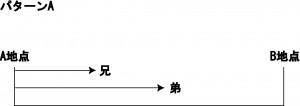
この場合は
わかっているもの
出会った時間または出会った距離
兄と弟の早さ
弟が先に出た時間
わからないもの
出会った距離または出会った時間
解き方
兄の早さ×出会った時間=弟の早さ×弟が先に出た時間+弟の早さ×出会った時間=出会った距離
兄の早さ×出会った時間=(弟が先に出た時間+出会った時間)×弟の早さ=出会った距離
求める場所によって難しさが変わってくる
パターンB
違う地点(同じ地点)から向かい合って進む
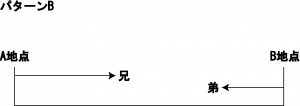
わかっているもの
出会った時間または出会った距離
兄と弟の早さ
わからないもの
出会った距離または出会った時間
※池の周りを反対方向進む問題も同じです
解き方
兄の早さ×出会った時間+弟の早さ×出会った時間=出会った距離
(兄の早さ+弟の早さ)×出会った時間=出会った距離
求める場所によって難しさが変わってくる
弟が先に出たりする応用問題がある
中間が終わったところですが、副教科は半分終わっています。
一旦、ここで副教科をまとめておくと期末前にバタバタすることはないでしょう!!
数学や英語は中間試験の内容をふまえたものになりますので中間試験でわからなかったところや間違えたところは今のうちにやり直すことをお勧めします
今回の中間試験で間違えたいる所を確認してわかっていなかったのかそれともミスで間違えたのかをはっきりしておくのも大切です!!
昨日に続いて本日は昼ごはんを食べてから勉強です!!
今回の数学はもっとも大事な方程式!!
つまづくとこれからが大変ですのでしっかり前もって教えました!!
計算はできても文章問題を式に直すのがやはり苦手!!
読解力不足です!!
○○を『X』として、計算式を立てます!!
数学できる人は計算しなくていい『X』なので楽ちんに思いますが数学を苦手とする人には『X』~~~
いや~~~って感じになります
数学は大丈夫だろうと思いまず英語からです!!
単語を覚えたり基本の文章を書いたりです
何となくわかっていないので少し説明をしました
英語は苦手です!!
三人称単数は簡単なようで難しい!!
動詞にsが付いたりして名詞の複数形と勘違いしているみたいです!!
なんとか理解できたのかなぁ?
ほんと語学はいろいろな言い回しや規則があってややこしい!!
少し息抜きの為に高校入試や我が家の勉強方法についておしゃべりしましたがおしゃべりの方が長かったような
幼稚園の次女は幼稚園に居残りでした!!
夕方までしてから晩御飯を食べて続きです
英語を少ししてから国語です
昨日の失敗をふまえて問題集の予想問題を解きましたが眠そう!!
今日は10時半までで終了です
続きは朝起きてからするそうです!!
それまでも少しずつ手伝っていましたが試験前日のお手伝い!!
夕方前に帰って来てお店で数学の提出用ワークを終わらせる
わからないところを仕事しながら教えました
幼稚園の次女はiPadでいろいろ遊びながら隣に座っていました!!
夕食を食べて明日の試験教科である理科と社会を始めました
お腹いっぱいで眠たそう!!
社会の提出用ノートをしたりプリントをしたり理科のプリントをしたり全然終わりません!!
とりあえず提出用のノートは終わりました!!
都道府県の県庁所在地は課題テストの後のテストで覚えていたので見直すだけ!!
地図記号は小学校で覚えたので見直すだけ!!
でも、やっぱり2学期の中間は範囲が広いです!!
別で買った問題集に予想問題があったのにさせるのを忘れてました!!
ふ~~~
やってしまいました!!
11時半までよく頑張りました!!
明日は朝起きて続きをするそうです!!
ファイト!!
最初の数と最後の数を足すと真ん中の2倍になる(数列の個数が奇数の場合に限る)
例えば
1,3,5,7,9,11,13
と並んでいると
1+13=14で7の2倍になる
これをXを使ってみると
真ん中の数をXとすると
x-6,X-4,X-2,X,X+2,X+4,X+6
(x-6)+(X+6)=2X
よって両端の数字の和は真ん中の数の2倍になる
これは規則的に並んだ数列であればどんな数列にも当てはまるものである
もう一つ例を言うなら
1,2,3,4・・・・・・99
と並んでいれば
1+99=100
100/2=50
と言うことは
1~99の真ん中は50と言う事がわかります
両端の和が真ん中の2倍ならば
両端を足して2で割れば真ん中の数字がわかると言うことです!!
では、数列の個数が偶数ならどうなるのか?
それは真ん中の数字がないので
小数になります
1,2,3,4・・・・・・100
なら
1+100=101
101/2=50.5
真ん中の数字は無く
50と51が真ん中の2つとなります
50+51=101になるのでわかると思います