2桁の掛け算


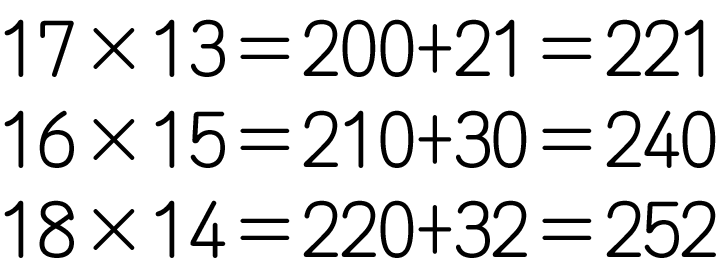

扇形は円の何分の1かがわかれば全部解ける
周囲は半径又は直径を使うが面積は必ず半径を使う
半径×2は直径
一次関数の一般的な式は
y=ax+bで表される
グラフを書くにはどうしたらいいのか
まず、点について考える
1点ならばそれは点だけ
2点ならばそれは線が引ける
3点ならばそれは平面が書ける
と言うことは
2点を見つければ
直線が引けてグラフが書ける
一番簡単なのは
(0,b)もう一つはy=0を代入して
(-b÷a,0)
一次関数の一般的な式は
y=ax+bで表される
aが傾き
bが切片
では、
y=axと何が違うのか
それはただ単にbが足される(引かれる)事
要はx=0(y軸)の時にb(切片)を通る
必ず(0,b)を通ると言う事
y=axとy=ax+bは平行である
例えば
(2,-7)を通り切片が3ならば
y=ax+bに代入して
-7=a×2+3
a=-5と解く
y=-5x+3になる
でも、他に一次関数の意味から解くと
(2,-7)を通り切片が3ならば
y=axに切片3が足された式なので
(2,-7-3)を通ることになり
x=2でy=-10
よって-10=a×2
a=-5となり
y=-5x+3になる
?°の所を求める問題です
まず、5角形の内角の和は180°×(5-2)=540°
ひとつの角は540°÷5=108°
まず?°を求めるには補助線を引いて錯角や同位角で求めれるようにする
?°を求めるには錯角である∠B’を求める必要がある
∠B’を求めるには∠Aを求める必要がある
∠Aを求めるには∠A’を求める必要がある
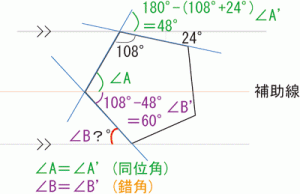
ただ、補助線を引かなくてもできる方法
まず、5角形の内角の和は180°×(5-2)=540°
ひとつの角は540°÷5=108°
上の線と正五角形の線が重なっていると考えると
下の角を挟む角は同じ角度になるので
180°-108°=72°
72°÷2=36°
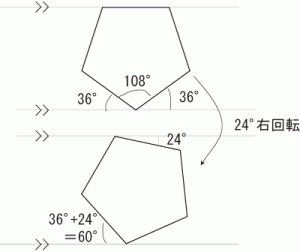
正五角形が24度回転したと考えれば
36°+24°=60°となる
備考
n角形の内角の和は180°×(n-2)
nの中には三角形がn-2個出来るからです
外角の和は必ず360°になります
5=10÷2に置き換える
1356×5=1356×10÷2
=1356÷2×10
1356を2で割る
1356÷2=678
それから後ろに0をつけると
678×10=6780
6780になる
1356×99=
1356(100-1)=13560
-1356
1356×105=
1356(100+5)=13560
+6780
1356×202=
1356×(200+2)=271200
+2712
1356×7=
1356×(5+2)=6780
+2712
昨年は合計で400人今年は男子が6%減少し、女子は18%増加した
全体で12人増えた
|
男子
|
女子
|
合計
|
|
|
昨年
|
X
|
400-X
|
400
|
|
今年
|
(1-0.06)X
|
(1+0.18)(400-X)
|
412
|
|
差
|
-0.06X
|
0.18(400-X)
|
12
|
昨年の男子をXとしたら昨年の女子は400-X
男子は6%減ったので-0.06X
女子は18%増えたので0.18(400-X)
去年より12人増えたので
-0.06X+0.18(400-X)=12
X=250
昨年の男子は250人
昨年の女子は150人
今年は男子は250×(1-0.06)=235(人)
今年は女子は150×(1+0.18)=177(人)
120円の定価で20円の利益を足していたら仕入れ値は100円
120-20=100(円)
仕入れ値100円に20%(2割)の利益を足した定価は120円
100×0.2=20 100+20=120(円) 又は100×(1+0.2)=120(円)
定価120円で仕入れ値に20%(2割)の利益を足していたら仕入れ値は100円
120÷(1+0.2)=100(円)
方程式 距離と速さと時間の問題はパターンAとパターンBしかない
まず、問題を読んでパターンAかパターンBになるかを考える
パターンA
同じ出発地点で同じ方向に進む
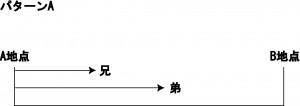
この場合は
わかっているもの
出会った時間または出会った距離
兄と弟の早さ
弟が先に出た時間
わからないもの
出会った距離または出会った時間
解き方
兄の早さ×出会った時間=弟の早さ×弟が先に出た時間+弟の早さ×出会った時間=出会った距離
兄の早さ×出会った時間=(弟が先に出た時間+出会った時間)×弟の早さ=出会った距離
求める場所によって難しさが変わってくる
パターンB
違う地点(同じ地点)から向かい合って進む
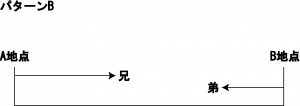
わかっているもの
出会った時間または出会った距離
兄と弟の早さ
わからないもの
出会った距離または出会った時間
※池の周りを反対方向進む問題も同じです
解き方
兄の早さ×出会った時間+弟の早さ×出会った時間=出会った距離
(兄の早さ+弟の早さ)×出会った時間=出会った距離
求める場所によって難しさが変わってくる
弟が先に出たりする応用問題がある
最初の数と最後の数を足すと真ん中の2倍になる(数列の個数が奇数の場合に限る)
例えば
1,3,5,7,9,11,13
と並んでいると
1+13=14で7の2倍になる
これをXを使ってみると
真ん中の数をXとすると
x-6,X-4,X-2,X,X+2,X+4,X+6
(x-6)+(X+6)=2X
よって両端の数字の和は真ん中の数の2倍になる
これは規則的に並んだ数列であればどんな数列にも当てはまるものである
もう一つ例を言うなら
1,2,3,4・・・・・・99
と並んでいれば
1+99=100
100/2=50
と言うことは
1~99の真ん中は50と言う事がわかります
両端の和が真ん中の2倍ならば
両端を足して2で割れば真ん中の数字がわかると言うことです!!
では、数列の個数が偶数ならどうなるのか?
それは真ん中の数字がないので
小数になります
1,2,3,4・・・・・・100
なら
1+100=101
101/2=50.5
真ん中の数字は無く
50と51が真ん中の2つとなります
50+51=101になるのでわかると思います
√2+√3=√5ならば(√2+√3)²=5になるはず
(√2+√3)²=(√2+√3)(√2+√3)=√2(√2+√3)+√3(√2+√3)=2+√6+√6+3=5+2√6
5にはならないので
√2+√3=√5にはならない事がわかる
よって√2+√3=√(5+2√6)になる
上記を√2=X √3=Yにすると
(X+Y)²=X²+2XY+Y²になることがわかる